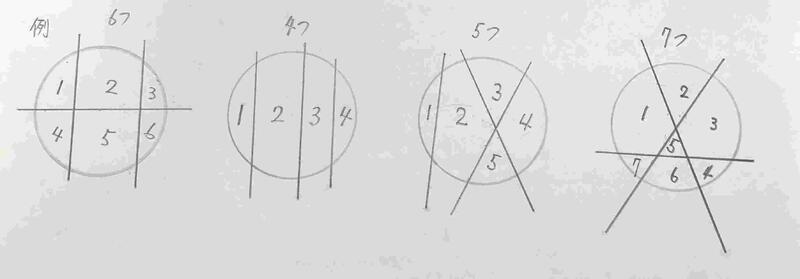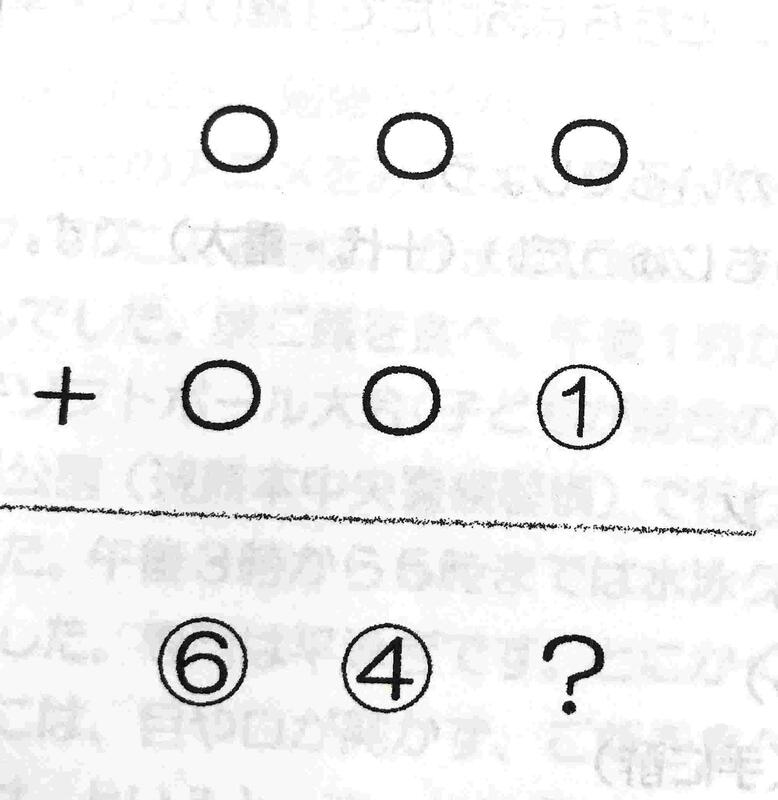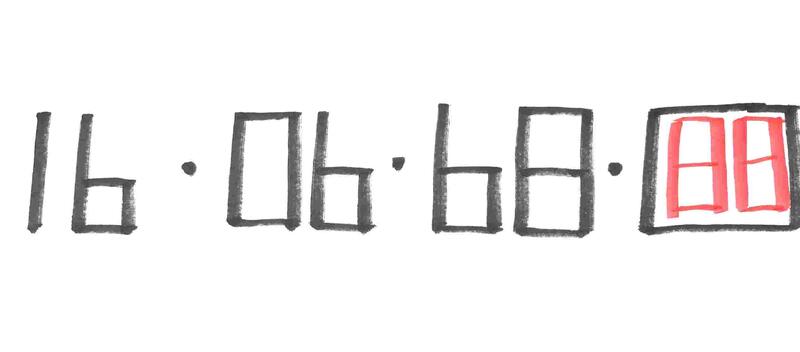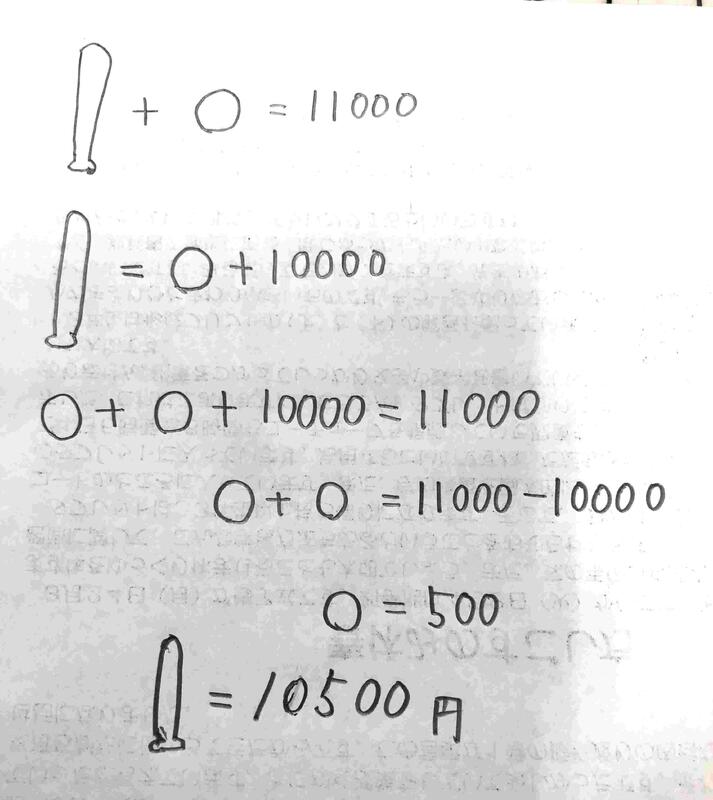よく雨が降りましたね。大丈夫だったでしょうか。今日は８月１２日です。１９８５年（昭和６０年）８月１２日、日航ジャンボ機墜落事故が起きました。亡くなられた方は５２０名でした。今日で丸４０年が経過します。当時、私は教員をしていました。テレビのニュース番組をみて、心がとても痛みました。また、飛行機の制御ができず、左右にぶれることを「ダッチロール」という言葉もこの時、はじめて知りました。４０年の歳月が過ぎましたが、昨日のように思い出します。ご冥福をお祈りいたします。

【算数おもしろ問題】今日の問題も算数オリンピックから引用しています。

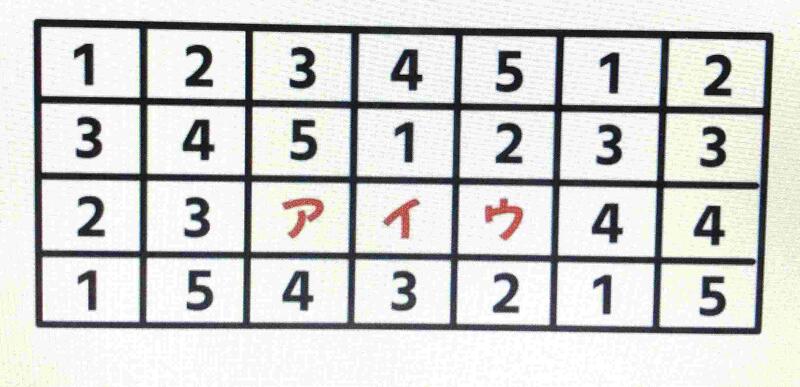
①下の表は、ある法則にしたがって数字が並んでいます。ア、イ、ウに入る数字を考えましょう。

②答えが１０になる２つの式があります。下の記号を使って、それぞれ正しい式にしましょう。（式の計算では、（　　）の中を最初にします。次に✖、÷、最後に＋、－になります。原則計算は左からおこないます。）

 解答

①

②

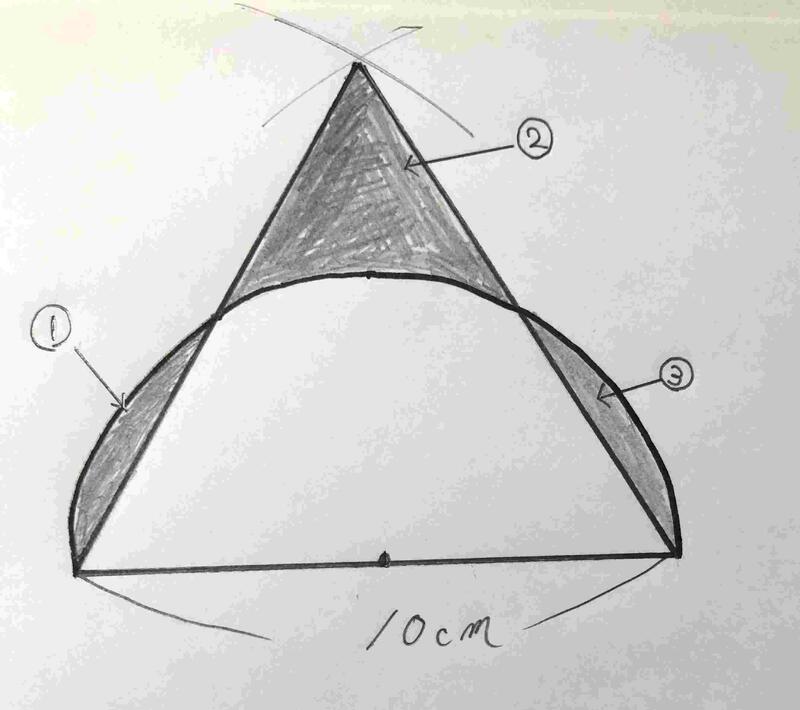
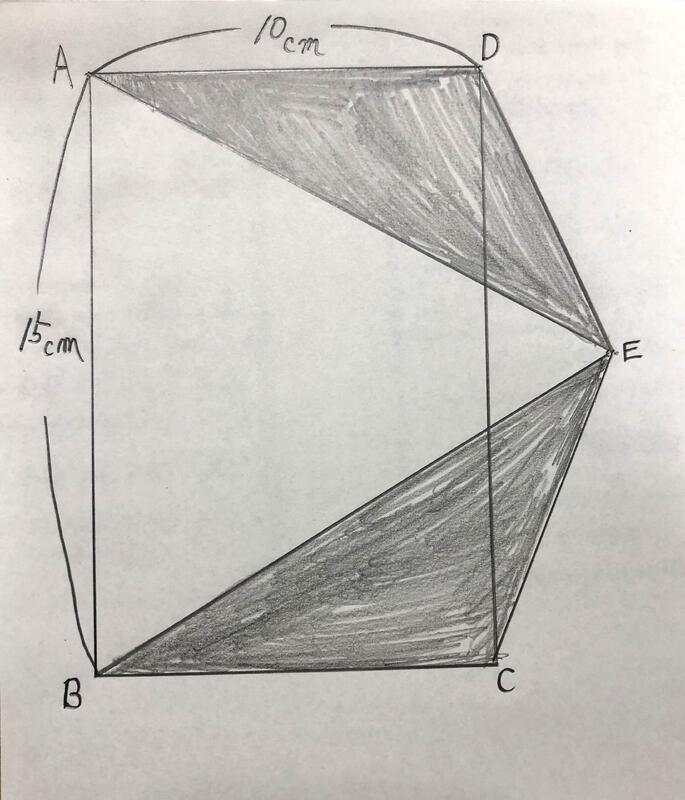
➂等積変形の問題です。下記の図のように１辺の長さが１０ｃｍの正三角形と直径が１０㎝の半円が重なっています。このとき、黒い部分の面積①、②、③を合わせた面積を求めましょう。ただし、円周率は３．１４とします。また、答えは小数第２位を四捨五入して、小数第１位まで求めましょう。

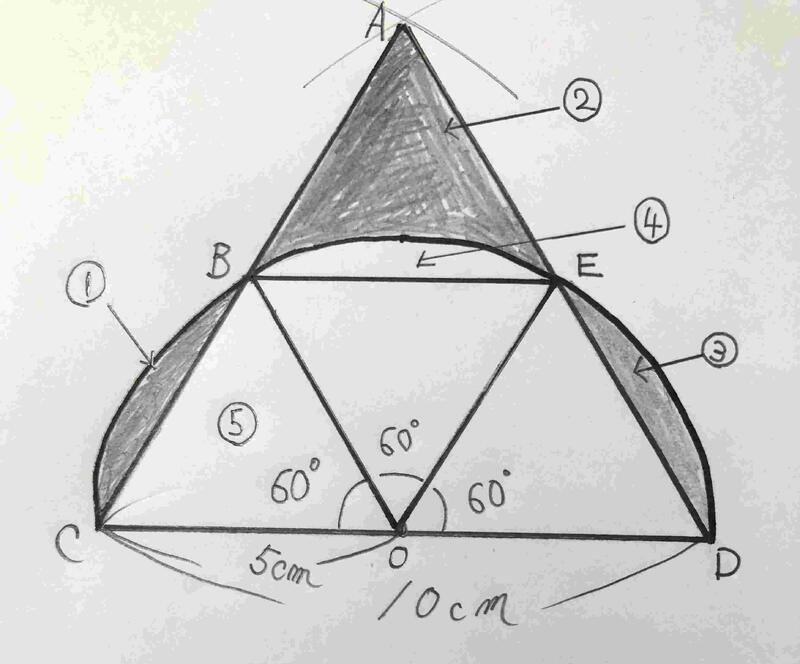
解答➂

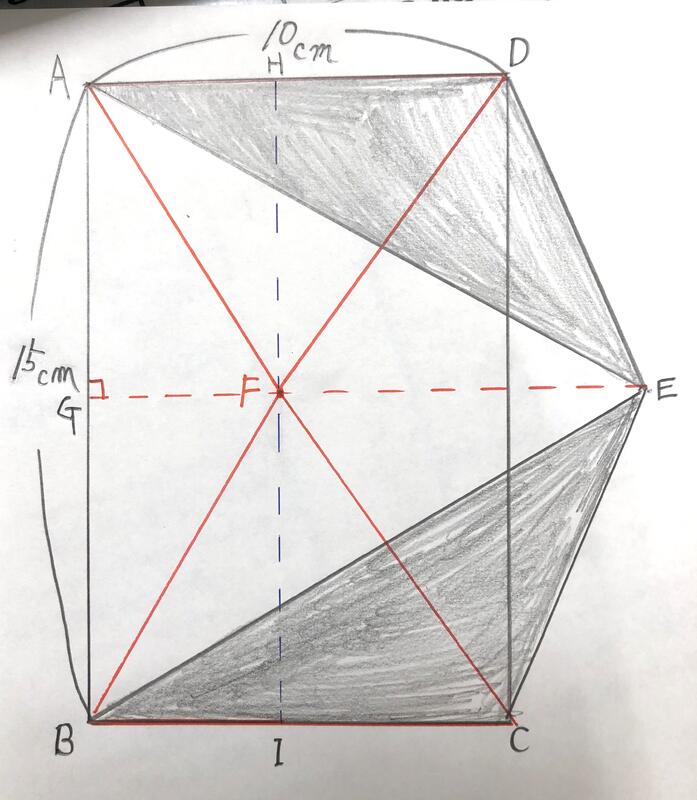
まず、半円の中心をOとして、１辺の長さが５㎝の４つの合同（ぴったり重なる）な三角形に分けます。次に③の部分を④に移動させます。三角形ABEの面積になります。三角形ABEの面積と三角形BCOの面積は等しいので、求めたい面積は半径５㎝、中心角６０度の扇形の面積を求めればよいです。よって、５×５×３．１４×６分の１＝１３．０８・・・

答え　約１３．１㎠

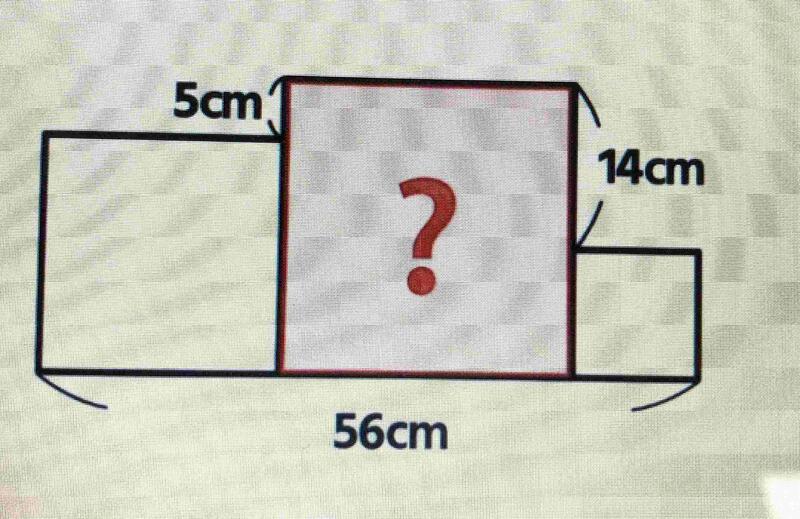
④下記のような３つの正方形があります。真ん中の正方形の１辺は何㎝でしょうか。

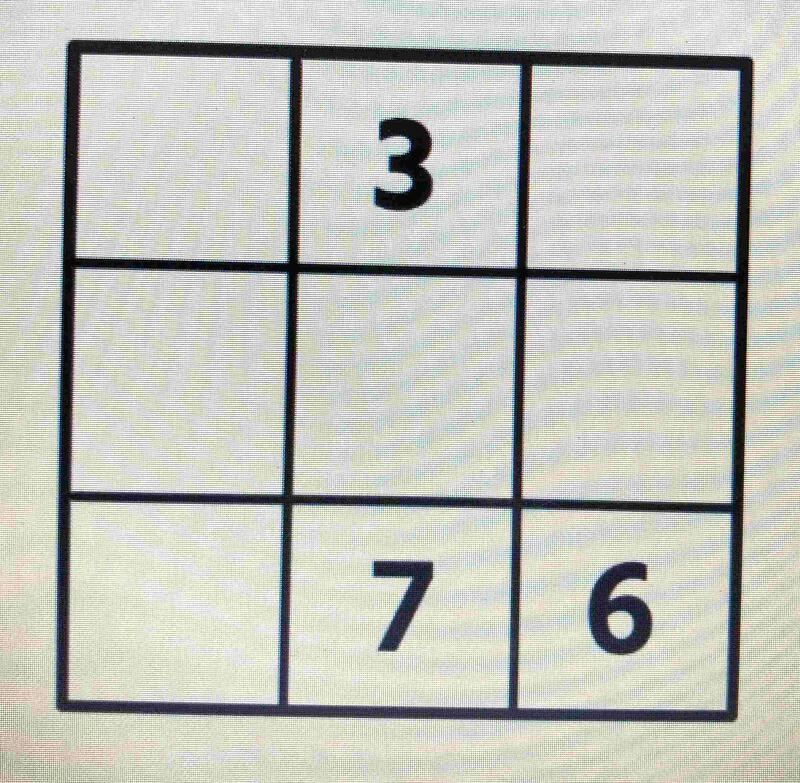
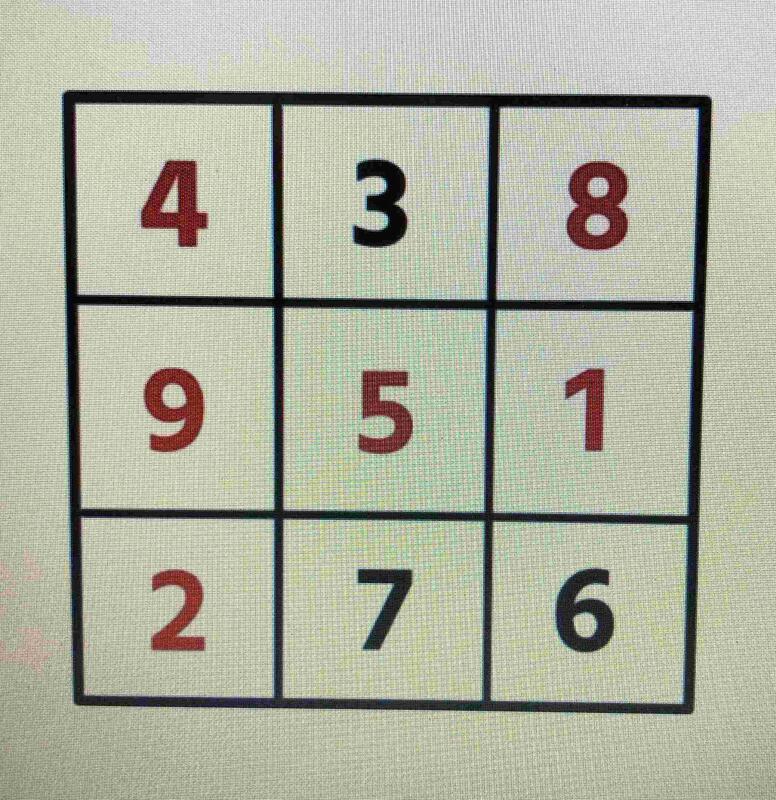
⑤１～９の数字を１つずつ入れて、縦、横、斜め３つの数字の和が同じになるようにしましょう。

解答

④答えの出し方はいろいろあります。その１例です。

中くらいの正方形の１辺の長さをA、１番大きい正方形の１辺の長さをB、１番小さい正方形の１辺の長さをCとおきます。A＋B＋C＝５６、A＝Bー５、Ｃ＝Ｂー１４に置きかえることができます。そこで、Ａ＋Ｂ＋Ｃ＝Ｂ－５＋Ｂ＋Ｂ－１４＝５６。３Ｂー１９＝５６。３Ｂ＝７５。よってＢ＝１５

答え１５㎝

⑤

【７回目　イチロー氏の言葉より】　

一日一日の積み重ねが　みたことのない　世界へつれていってくれる

今日は、日本プロ野球、アメリカ大リーグで活躍された鈴木一郎氏の話をさせていただきます。

最初、私が感銘を受けた言葉は、野球の理論のことです。通常ボールをいかにうまくバットに当てるかを考えます。当時イチロー氏が言った言葉は「２ストライクまで追い込まれたら別だが、それまでは、打ちにいって、自分の考えと違ったボールがきたら、空振りする技術を身につけていると話されました。つまり、打ちにいって、ボテボテのゴロだったらアウトになる確率が高い、それよりも空振りする方が次につながると話されていました。発想の違いを感じました。

先日イチロー氏のアメリカ大リーグ殿堂入りのセレモニーが行われました。すべての人々に対して感謝の気持ちを話されていました。時にはジョークも交えた和やかなスピーチでした。すばらしかったですね。昨年殿堂入りのインタビューを受けられた時、子どもたちに次のようなメッセージを送られていました。

①大きな成果（せいか）をあげるには、いっきにそこへはいけない。地道に毎日をつみ重ねることが、大きな成果をあげる道である。

②人はだれでも才能（さいのう）を持っている。しかし、その才能を花開かせるのは、その人の毎日の努力である。

と話されていました。

５～６年前、現役を引退されたイチロー氏がテレビ出演をされていました。「教えてイチロー先生」というテレビ番組です。イチロー氏が子どもや大人相手に、質問を受け、それに答えていらっしゃいました。その中で、子どもから、こんな質問がありました。「宿題はなぜしなければいけないのですか。」という質問です。それに対しイチロー氏は「私も宿題はいやでした。しかし、大人になってから、いやなことをしなければならないことが沢山あります。その時の練習と思って取り組めばどうでしょうか。」と話されていました。なるほど、一つの考え方ですね。

次にこんな質問もありました。「出る杭は打たれるといいますが、どうすればよいでしょうか。」という質問です。イチロー氏は「出る杭は打たれますが、出すぎる杭は打たれません。」と話されました。この答えを聞いていた時、私は少し顔がほころびました。それは、２０数年前から、私が言ってきたことと、イチロー氏が答えられたことが、一緒だったからです。１０数年間ほぼ毎日、ホームページを更新（こうしん）しています。最初の方は、「そんなことは無駄（むだ）な事」などという声も聞きました。しかし、続けていくとそのような声が小さくなりました。出る杭は打たれます。しかし、出すぎた杭は打たれなくなります。継続は力です。でも、出すぎた時に気をつけなければならないことがあります。それは、謙虚（けんきょ）さが必要になります。出すぎることはいいことですが、同時に謙虚さも兼（か）ね備（そな）えなければいけませんね。

最後に、他人から嫌（きら）われるのは大好きだとも話されていました。一番いやなことは、興味（きょうみ）がないこと、無関心なことが一番つらいと話されました。心にしみる話でした。

【８回目　ひとつのことば　】

北原白秋先生は、１８８５年生誕、１９４２永眠されました。詩人でもあり童謡作家でもあり歌人でもあられました。お母様は熊本の南関町出身の方です。熊本にもゆかりのある方です。「あめあめふれふれ　かあさんが」で知られる「あめふり」など聞かれたことがあるかもしれませんね。白秋先生の作品の中に「ひとつのことば」というものがあります。これは、いかにことばが大切で、いかにことばが人を傷つけるかなど、ことばの大切さが詩の中に凝縮しています。「ひとつのことば」目にしていただくと幸いです。

【９回目　マシュマロ実験】

アメリカのスタンフォード大学で１９７０年代に行われた実験です。４歳の子どもたち１８６人が実験に参加しました。机の上にはさらがあり、マシュマロが１このっています。実験者は「私はちょっと用がある。それはきみにあげるけど、私がもどってくるまで１５分間、食べるのをがまんしていたら、マシュマロをもう１つあげる。私がいない間に食べたら、２つめはなしだよ」と言って部屋を出て行きました。最後までがまんして、２こめのマシュマロを手に入れた子どもは３分の１程度でした。

その後ついせき調査をし、マシュマロを食べなかったグループは、まわりから、より優秀と評価され、大学進学適性試験でも点数がよかったそうです。この傾向が、ずっと後の人生に継続していることがあきらかにされました。（生涯年収もよかったそうです。）

自分の衝動（しょうどう）や感情をコントロールし、目先の欲求（よっきゅう）をしんぼうする能力（のうりょく）は、人が社会で成功するうえで、重要であることを意味している実験です。がまんできることは、その人が将来よりよい人生をおくるのに重要なことを言っています。

すべて「がまん・がまん」ではありませんが、がまんする気持ちはその人を大きく成長させる行動ですね。

【本日も多くの職員が出張に出かけています。午前９時から３０分間電気工事のため、停電になりました。その間、校舎内外の清掃活動をしました。】

【明日は８月９日です。昭和２０年８月９日、午前１１時２分、原子爆弾「ファットマン」が長崎市上空に投下されました。一瞬のうちに多くの方々が亡くなられ、多くの方々が今なお後遺症に苦しんでいらっしゃいます。今年は戦後８０年です。平和の大切さ、戦争の悲惨さを一人一人がじっくり考えるいい機会だと思います。】

【昨日の雷すごかったですね。本校には私（昭和３２年生まれ）と同年代の職員が、私を含めて３人います。職員室で昼ご飯を食べている時です。私が小さい頃、雷が鳴ったら、蚊帳（かや）を張り、その中に逃げていた話をしました。２人の先生方にも共感してもらいました。その後、熊延鉄道の話。また、熊本市内では、現在市電は田崎～健軍間・上熊本～健軍間の２つの路線ですが、私たちが小さい頃には、川尻線や子飼線に乗った話などもしました。最後には、どこどこに映画館があった話やどこどこにボーリング場があった話などで盛り上がりました。】

【算数おもしろ問題】

①   おこづかいの問題です。あなたが１か月にもらうおこづかいを決めるならば、どちらのおこづかいのもらい方を選びますか。

A：毎月、１日（ついたち）に１万円もらうもらい方。

B：１日に１円もらう。２日には２倍の２円。３日には２円の２倍の４円。４日には４円の２倍の８円というように、毎日、前日の２倍のおこづかいをもらうもらい方。ただし、月の半分の１５日で終わりにします。AとBどちらのもらい方を選びますか。筆算や電卓等で計算してみてください。

解答

①１日目１円→２日目２円→３日目４円→４日目８円→５日目１６円→・・・→１５日目１６３８４円になります。１５日間の合計金額は３２７６７円です。あなたはどちらを選びましたか。

②　三角形の面積を求める問題です。三角形の面積は底辺×高さ÷２で求めることができます。そこで、下記の２つの三角形の黒い部分を合わせた面積を求めてみましょう。これは等積変形といって、面積を変えずに形を変えて考える問題です。

②解答

Eを通り、辺ADに平行な直線をひきます。その直線上に点Fをとります。△AEDと△AFDは底辺が同じで、高さも等しいので面積が同じになります。同様に△BEC＝△BFCになります。△AFHは長方形AGFHの半分の面積です。同様にして、△AFD＋△BFCの面積は長方形ABCDの面積の半分になります。よって、△AED＋△BEC面積は１５×１０÷２＝７５　答え７５㎠になります。

➂    クイズです。１００―１＝何色でしょうか。（ヒント：漢字）

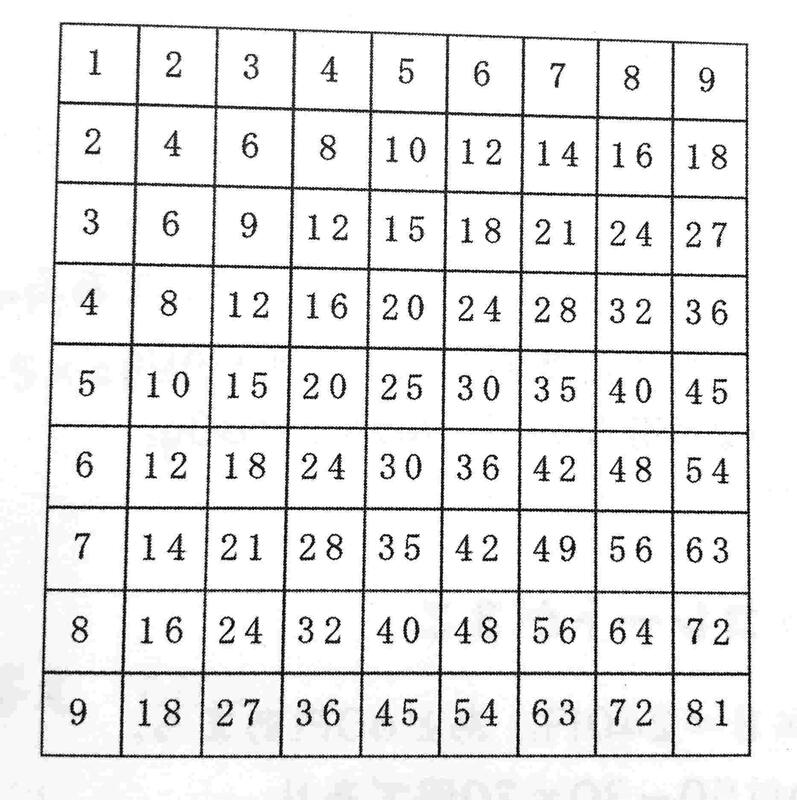
④   下のかけ算九九表にある数字を全てたしたらいくつになるでしょうか。規則性を見つけ、計算で求めてみましょう。

⑤円に直線を３本ひいて、いくつかに分けます。下の図のように、６つに分ける分け方があります。他に、４つ・５つ・７つに分ける分け方を考えてみましょう。

⑥ 読解力を高める問題です。頭の中で考えることもいいですが、順番に整理すると、考えやすくなりますよ。問題：一郎さん、花子さん、太郎さんがそれぞれ色紙を持っています。一郎さんは８０枚、花子さんは一郎さんより５枚多く、太郎さんは花子さんより７枚少なく持っています。３人の枚数を同じにするためには、花子さんから一郎さんと太郎さんへそれぞれ何枚わたせばよいでしょうか。

⑦論理的に考えていく問題です。Aさん、Bさん、Cさん、Dさんはどこの国の人でしょうか。下記の文を読んで考えてみましょう。

①    ４人は、日本人、アメリカ人、イギリス人、フランス人です。

②    Aさんは、アメリカ人ではありません。

③    Bさんは、フランス人ではありません。

④    Aさん、Dさんは、アメリカ人か日本人です。

解答

➂１００ー１＝百ー一＝白　白色でした。

④１の段は１＋２＋・・・＋８＋９＝４５になります。２の段は４５×２＝９０、３の段は４５×３＝１３５、・・・、９の段は４５×９＝４０５です。すべてをたすと４５×（１＋２＋・・・＋８＋９）＝４５×４５＝２０２５になります。

⑤

⑥まず、３人の持っている枚数を考えてみます。

一郎さん８０枚、花子さん８５枚、太郎さん７８枚になります。次に３人の枚数を同じにするので、（８０＋８５＋７８）÷３＝２４３÷３＝８１。３人が８１枚になればよいので、花子さんから一郎さんへ１枚。花子さんから太郎さんへ３枚わたせば、３人の枚数が一緒になります。

 ⑦　②と④から、Aさんは日本人であることがわかります。その結果、Dさんがアメリカ人ということも分かります。残るはBさんとCさんです。イギリス人かフランス人になりますが、➂からBさんはイギリス人、残ったCさんがフランス人というのが分かります。

【５回目　愛、深き淵より】４０数年前はパソコンもなければ、インターネット通信などもありません。情報は紙媒体が主流です。教員になってすぐ、国語、算数、理科、社会、・・・道徳、学級活動、児童会、クラブ活動・・・などをまとめてあった本がありました。当時数十万円したと思いますが購入しました。また、１年１組せんせいあのね（鹿島和夫先生）や兔の目（灰谷健次郎先生）、また甲佐町出身の丘修三先生の「ぼくのお姉さん」などもよく読んでいました。そんな中、友人から星野富弘さんの「愛、深き淵より」を教えてもらいました。星野さんが、１９７０年群馬県の中学校で体育教師になられたばかりの頃です。放課後のクラブ活動で、器械体操の指導中、頸髄（けいずい）を損傷し、手足の自由が失われました。その後、口に筆をくわえ、詩画集をだされた人物です。とにかく衝撃を受けたことを覚えています。入院されている星野さんは、お母さんと大げんかをされていました。その時、１ぴきのハエが星野さんの顔の上をぶんぶん飛んでいます。大げんかをしていたにもかかわらず、お母さんは、手でそっとハエを払ってくれました。感動する文や言葉、絵がたくさんあります。星野さんが熊本県立美術館に来られた時、会いに行ったことを覚えています。詩画集「風の旅」や「かぎりなくやさしい花々」の本も購入しました。令和６年４月２８日、星野富弘さんが永眠されました。

【６回目　ピグマリオン効果とゴーレム効果】

保護者の皆様、「ピグマリオン効果」という言葉を聞かれたことはありますか。ピグマリオン効果とは、教育心理学の用語で、他者から期待されると成績が向上する現象（げんしょう）をいいます。「頑張っているね。」「すごく伸びてきているよ。」「さすがだね。」「すごいね。」「さらにあなたはよくなるよ。」など多くの肯定的な言葉をかけることにより、子どもたちは、さらにがんばろうとする力が倍加します。

しかし、ここで教員は注意しなければいけないことがあります。一人の児童ばかりに声かけをして、不公平を生まないようにすることです。クラス全員の児童に、それぞれのよいところ、がんばっているところなど声かけをし、伸ばしていくことが大切です。家庭でも子どもたちのよさにしっかり声をかけてもらうと嬉しいです。

逆に、期待されないことで、成績が低下する現象を「ゴーレム効果」といいます。ゴーレム効果にならないように、子どもたちのよさやがんばりを多いに褒（ほ）めていきたいですね。家庭でも子どもたちをたくさん褒めてください。褒めることがないと言われるご家庭は、褒める場や機会をつくって、子どもたちを褒めてください。ご協力よろしくお願いします。

【今日は「立秋」です。暦の上では秋の始まりですね。また、夏休みがちょうど半分がすぎました。いかがお過ごしでしょうか。最近の雨で、少し過ごしやすくなったかなあと感じていますが、まだまだ暑さが続くと思います。体調に気をつけてお過ごしください。】

 【学校で飼育しているメダカも気持ちよさそうに泳いでいます。】

【算数おもしろ問題】

①１～９までの数字を１回ずつ使って、たし算の筆算を完成させ、？に入る数字を求めましょう。

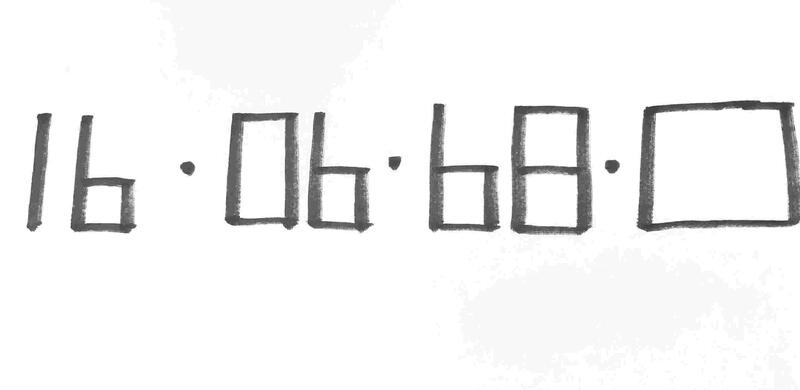
②車が止まっている駐車場の番号を、規則性を見つけて▢の中の番号を考えてみましょう。

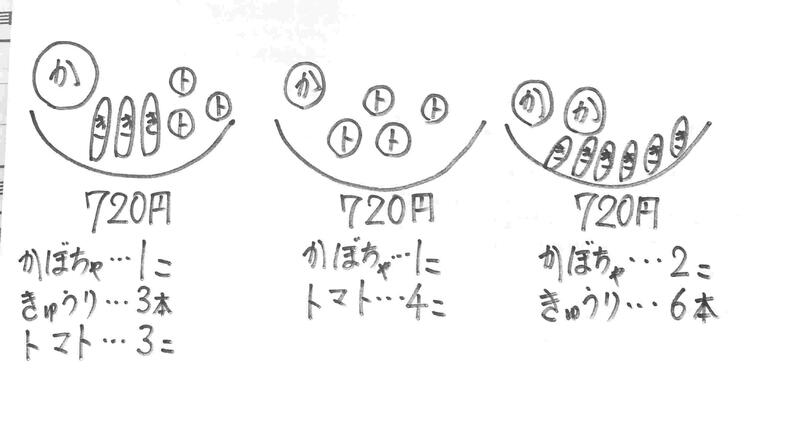
➂八百屋さんに行くと、かぼちゃ、きゅうり、トマトを下のように売っていました。どれも、ざる１つ分が７２０円です。かぼちゃ、きゅうり、トマトそれぞれ１個のねだんを考えましょう。ただし、ざるのねだんは考えないものとします。（置きかえて考えるといいかもしれませんね。）

④もう１問置きかえて考える問題をだします。ある日のことです。昼の時間は、夜の時間より１時間長かったです。昼と夜の時間はそれぞれ何時間だったでしょうか。（昼の時間を〇、夜の時間を▢とおいて考えるといいかもしれませんね。）

⑤つるかめ算という問題をだします。どういうものかというと、もしもの場合を考えて、答えを導き出すものです。問題です。つるは足が２本、かめは足が４本です。つるとかめが合わせて１６ぴきいます。その足の数の和は５０本です。つるとかめはそれぞれ何匹いますか。

解答

①

？＝８でした。

②逆から見るといいですね。９１→９０→８９→８８になります。

➂「置きかえてみる」というところがポイントになります。かぼちゃを●、きゅうりを▲、トマトを○で表すと、

①・・・・・●　　▲▲▲　　　○○○＝７２０円

②・・・・・●　　            　　○○○○＝７２０円

③・・・・・●●    ▲▲▲▲▲▲        ＝７２０円

①と②から○＝▲▲▲

③の▲▲▲▲▲▲を○で表すと、

▲▲▲▲▲▲＝○○

つまり、③は●●○○＝７２０円

これと②と③から●＝○○

②をすべて○で表すと、

○○○○○○＝７２０円                    

○＝７２０÷６＝１２０円

●＝○○＝１２０×２＝２４０円

○＝▲▲▲より、▲＝１２０÷３＝４０円

答え　かぼちゃ・・・２４０円      きゅうり・・・４０円　

          トマト・・・１２０円

④昼の時間を〇、夜の時間を▢と置きかえてみます。わかっていることは、〇＋▢＝２４。〇＝▢＋１です。そこで、〇＋▢＝２４に〇＝▢＋１に置きかえると、▢＋１＋▢＝２４。▢＋▢＝２３。よって▢＝１１．５。〇＝１２．５。つまり、昼の長さは１２時間３０分。夜の長さは１１時間３０分です。

⑤例えば、全部がつるだったらと仮定します。足の数は２本×１６ぴき＝３２本です。実際、足の数は５０本なので、５０―３２＝１８本多くならなければなりません。かめはつるより２本足が多いです。よって１８÷２＝９。かめは９ひき、つるは７羽になります。

【４回目　ハインリッヒの法則（１：２９：３００の法則）】 

「ハインリッヒの法則」や「ヒヤリ・ハット」ということばをご存じですか。「ハインリッヒの法則」とは、１件の重大事故の裏には２９件の軽微（けいび）な事故と３００件のけがにいたらない事故（ヒヤリとしたりハットしたりすること）があるということです。別な言い方では「１：２９：３００の法則」とも呼ばれています。本校では、子どもたちが安全に、安心して過ごせるよう、毎月第１週目は、校内安全点検を実施しています。校内安全点検は、複数の職員で、運動場の遊具の点検をしたり、教室や廊下に危険物がないか、チェックをしたりしています。危険物があれば、すぐ取り除いたりします。また、子どもがけがをした場合は、現場に行き、状況を把握（はあく）し、どのようにしてけがが起きたか、全職員に知らせます。その後各担任から事故が再度起きないよう指導が行われます。児童にけがはなかったがヒヤリとしたとき、ハットしたときも、職員間で情報の共有化を図ります。「ハインリッヒの法則」に基づいて考えると、重大事故を防ぐには、軽微な事故やヒヤリとしたこと、ハットしたことの対策（たいさく）を行うことが有効だと言われています。学校もこの法則に従（したが）い、ヒヤリとした事例やハットした事例を出し合い、子どもたちに事故が起きないよう、日々対策をこうじています。学校は安全・安心が第一ですね！

【昨日は、群馬県伊勢崎市で、日本最高気温４１．８度が記録されました。熊本も最近は時々雨が降り、過ごしやすい時もありますが、まだまだ暑いです。体調に十分気をつけお過ごしください。】

【今日は８月６日です。今から８０年前、昭和２０年８月６日、午前８時１５分広島市にB-29戦略爆撃機「エノラ・ゲイ」により、原子爆弾「リトルボーイ」が投下されました。被ばくから４か月以内に亡くなられた方々は、約９万～１６万６０００人と言われています。私が小学生の頃は、夏休み期間中、８月６日か８月９日に「平和登校日」が設けてありました。その日は学校に行き、平和について学習していました。戦後８０年経ちます。「平和」について、もう一度考えてみるいい機会ですね。】

【本日は、御船町全員研修会が、御船中学校でおこなわれました。映像は本日の職員朝会の様子です。】

【算数おもしろ問題】

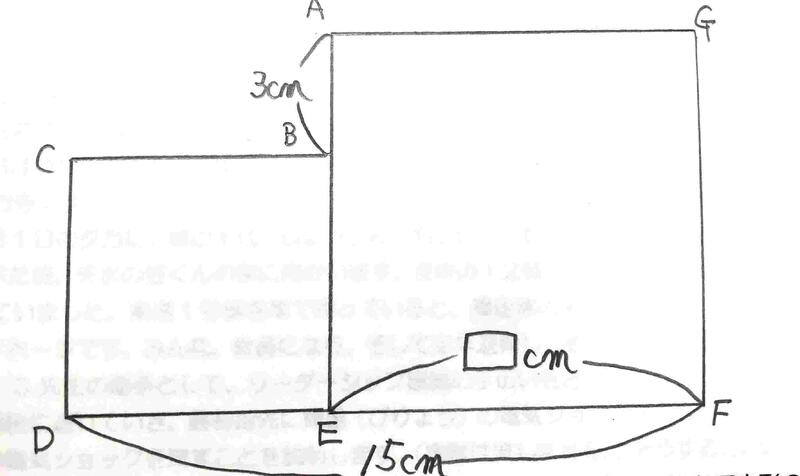
①正方形の面積の求め方は１辺×１辺です。下記の２つの正方形BCDEと正方形AEFGをあわせた面積を求めましょう。わかっているのはABの長さ３㎝、DFの長さ１５㎝だけです。EFの長さを▢と考えて問題にチャレンジしてみたらいいですね。

②１から９まで書いてあるカードが１枚ずつあります。これをＡくん、Ｂくん、Ｃくんの３人に、３枚ずつ配ったところ、３人とも、カードをたした合計の大きさが同じになりました。Ａくんは１、Ｂくんは２と４を持っていました。Ｃくんのカード３枚を答えてください。

③クイズです。昔の長さの単位で１里（り）は約４㎞です。３６㎞ある野菜は何でしょうか。

④長さ３０㎝のひもを切って、Ａ、Ｂ、Ｃの３本に分けると、ＡはＢより５㎝長く、ＢはＣより２㎝長くなりました。Ａ、Ｂ、Ｃそれぞれの長さは何㎝でしょうか。

⑤太郎くんは、野球用品でバットを１本とボールを１個買いました。ねだんは２つ合わせて１１０００円で、バットのねだんはボールのねだんより１００００円高かったそうです。ボールのねだんはいくらだったでしょうか。（ヒント：ボールのねだんは１０００円ではありませんよ。図をかいて考えるといいですね。）

解答

①最初ABの長さ３㎝に目をつけます。ABの長さは大きな正方形と小さな正方形の１辺の長さは▢―３で表すことができます。EF＝▢、DE＝▢―３、DFが１５㎝なので▢＋▢―３＝１５。▢＋▢＝１５＋３＝１８。▢＝９㎝ということがわかります。そこで小さい方の正方形の１辺は９－３＝６㎝。よって、６×６＋９×９＝３６＋８１＝１１７。答え１１７㎠という結果を導きだすことができます。

②１から９までを全てたすと４５になります。４５を３人で分けると１人は１５になります。Ｂくんは２と４を持っているので、残りは９です。Ａくんは９が使えないので、１＋▢＋〇＝１５。▢と〇には６と８が入ります。あまった３と５と７がＣくんの持っていたカードになります。

③３６㎞＝９里。よって「きゅうり」でした。

④AとBのひもを、Cのひもと同じ長さにします。そうするとAのひもはCのひもより２㎝＋５㎝＝７㎝長いです。BのひもはCのひもより２㎝長いです。だから、Cのひもより合計７㎝＋２㎝＝９㎝長くなっています。よって３０㎝―９㎝＝２１㎝。２１㎝÷３＝７㎝。Cのひもが７㎝とわかったので、Bのひもは、７㎝＋２㎝＝９㎝。Aのひもは７㎝＋７㎝＝１４㎝になります。

⑤

 ボールが５００円です。ちなみにバットは１０５００円です。

 【３回目　ゆっくり力】１０数年前「ゆっくり力ですべてがうまくいく」という本を読みました。著者は斎藤茂太（さいとうしげた）さんです。斎藤茂吉さんの長男さんです。精神科医・医学博士です。全部で８２の文章から成り立っていました。教師としての立場、親としての立場、一人間としての立場、様々な立場から読ませて頂きました。共感するところが多数ありました。この本の中では、人もお酒もゆっくり熟成する、子どもは一夜では育たないこと等が書かれてありました。「ゆっくり力ですべてうまくいく」子育てに何かヒントを与えてくれると思います。

【夏休み期間中でも、運動場や体育館等の安全点検をおこなっています。】

【本格的に貯水タンクの設置作業が始まりました。】

【棚の上や高いところなど、日頃できない所の掃除をしています。】

【中庭の汚れを、高圧洗浄機を使ってきれいにしています。】

【算数おもしろ問題】

①２＋４＝２４　この式に線１本入れて正しい答えにしましょう。

②電卓を用意してください。

１２３＋３６９＋９８７＋７４１＝を入力すると２２２０になります。次に１４７＋７８９＋９６３＋３２１＝を入力してみてください。規則性を見つけ、他にも、２２２０になる場合を見つけると楽しいですよ。

③途中の式を考えながら、式のきまりをみつけ、(　　　）の中の数をみつけましょう。

                   ０×９＋１　＝　１

                   １×９＋２    ＝　１１

           　 １２×９＋３   ＝　 １１１

             １２３×９＋４  ＝     １１１１

      　１２３４×９＋５  ＝　 １１１１１

     １２３４５×９＋６　＝  １１１１１１                                          

　（　　　　　　　　　） ＝  １１１１１１１

１２３４５６７×９＋８＝（　　　　　　　　　）　

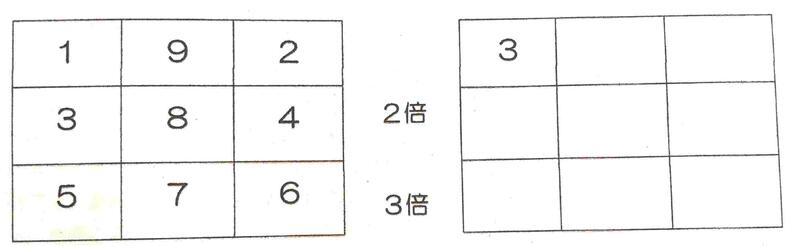
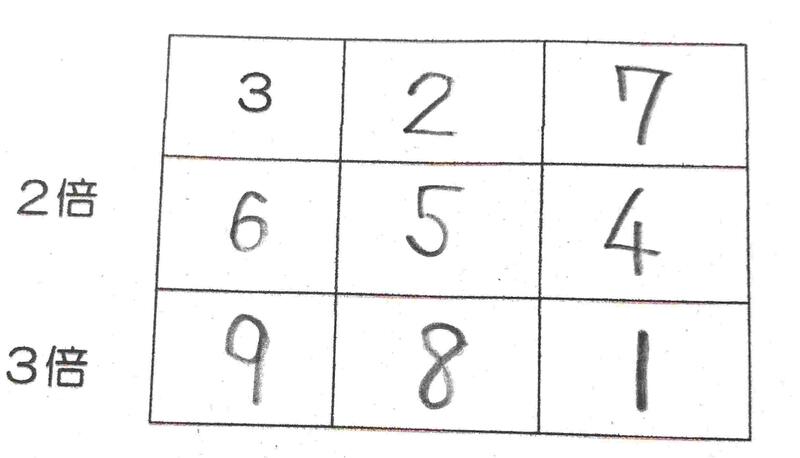
④３段に並んだ９個の数字１から９までの数字を１個ずつ、下の図のように並べます。すると、上段の１９２を２倍した３８４が中段に現れ、下段に５７６が現れます。同じ方法で、上段の左端に３を入れたときの並べ方を作ってください。

⑤１から６までの数字を１つずつ使って、下の式を完成させましょう。

▢▢✖▢＝▢▢▢

解答

①この問題も、子どもたちの概念を壊したいですね。線と言ったら、直線でも曲線でも線は線ですね。よって０を入れて、２０＋４＝２４にします。

②例えば１５９＋９６３＋３５７＋７４１＝２２２０などがあります。

③１２３４５６×９＋７）

　（１１１１１１１１）

④

 ⑤５４✖３＝１６２

【２回目　ブロークンウインドウ理論】今回は「ブロークンウインドウ理論」を紹介します。日本名「割れ窓理論」といいます。１台の車はきれいなまま、何もしないで放置しておきます。もう一台の車は、窓ガラスを割って放置しておきます。そうすると、窓ガラスを割って放置して置いた車の方は、すぐにタイヤ、ラジエター、バッテリーなどがとられたそうです。２４時間でほとんど金目のものはなくなったということです。それに対し、きれいにしておいた車は、１週間以上誰も手をつけなかったそうです。この実験はアメリカで行われました。この理論を「ブロークンウィンドウ理論」といいます。以前ニューヨークの地下鉄は落書きがいっぱい書いてあったそうです。しかし、この理論をもとに、徹底的に落書きを消した結果、犯罪が激減（げきげん）したとのことです。ただ、この考え方も賛否両論あり、全てが正しいということではありません。学校環境におきかえてみましょう。教室がきれいに整理整頓されている場合、そのクラスの支持的風土が高まります。学習に関しても考えが深くなっていきます。４０数年前、教師になった頃、年配の先生方から、「子どもたちが帰ったら、いつも教室は掃除をしとかなんばい。」と言われていたことを思い出します。整理整頓された環境は、子どもを大きく育てると考えています。

【午前６時４０分頃から雨が降り出しましたね。植物にとっては恵みの雨だったのではないでしょうか。また、小さな生き物にとっても恵みの雨だったと思います。午前８時頃の運動場の様子です。】

【算数おもしろ問題】

①   １から１００まで全部足したらいくつになるでしょうか。

②  同じ長さの線香が２本あります。１時間でちょうど１本燃え尽きます。これを使って、４５分間を計りましょう。

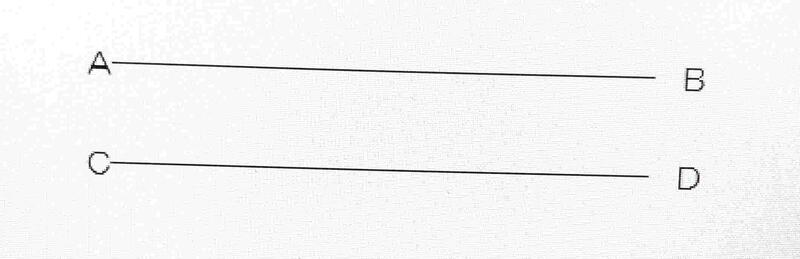
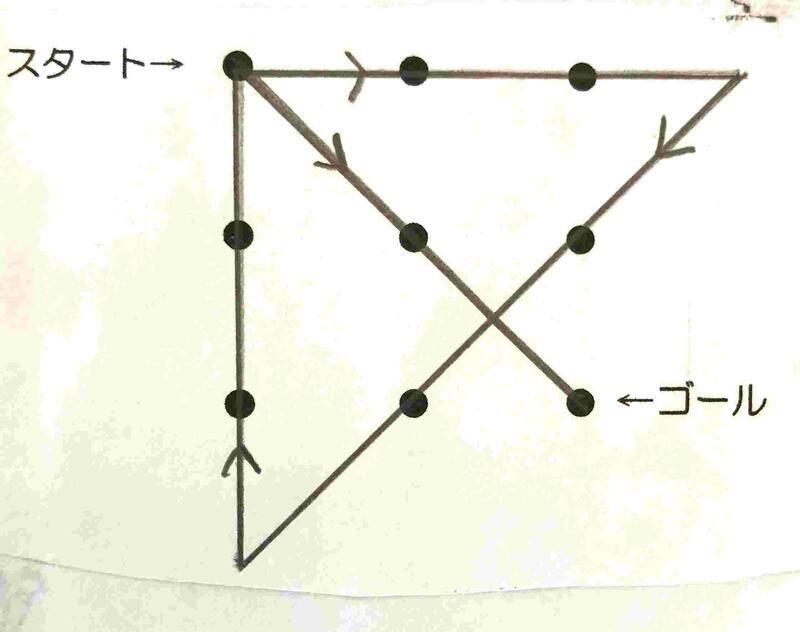
③  次の問題は、子どもたちの概念を壊したいと思って出しています。問題：９つの黒い点を、直線で、一筆書きで全ての●通ってください。ただし、３回しか角度をかえることはできません。つまり４本の直線で全ての●を通ります。（ヒント：わくからはみ出しましょう。）

④  １、１、２、３、５、８、１３、２１、□、５５、８９、・・・」という決まりを持った数字が並んでいます。決まりをみつけ□に入る数字を考えてみましょう。

⑤０から９までの整数から４つの数を選び、文字におきかえて式をつくりました。A、B、C、Dにあてはまる数を求めましょう。

（ヒント：最初十の位に着目して考えてみてください。）

解答

①ドイツの数学者ガウス氏は、7歳の時、算数の授業中教師から「１から１００までの数字をすべて足すといくつになるか。」という問題を出されました。ガウス少年は数秒で「５０５０」と答えたそうです。考え方は１と１００で１０１、２と９９で１０１、・・・５０と５１で１０１。つまり１０１のかたまりが５０個、１０１×５０＝５０５０と考えたそうです。別な説では１＋２＋３＋・・・＋９８＋９９＋１００の下に１００＋９９＋９８＋・・・３＋２＋１と書いて上下を足すと、１０１が全部で１００個なので１０１００。その半分だから１０１００÷２＝５０５０と考えたという説もあります。７歳のガウス少年すごいですね。

 ②   A、B、C同時に火をつけます。AーBが燃え尽きた時が３０分です。その時、Dに火をつけます。Dに火をつけてC－Dがもえつきた時間は１５分です。よって最初からは４５分になります。

③

④  この数の並びを、フィボナッチ数列といいます。イタリアの数学者フィボナッチにちなんで名付けられた数列です。前の２つの数字を足すと、次の数字がわかります。□＝１３＋２１＝３４になります。フィボナッチ数列は、様々なところで活用されています。例えば長方形の面積だったり、黄金比だったりします。詳しくは個々で調べてみてください。

⑤十の位に注目しましょう。C＋D＝Cなので、D＝０または、一の位から１繰り上がるとき、D＝９になります。D＝０のとき、一の位の等式が成り立ちません。したがって、D＝９ということがわかります。次に、千の位と一の位に注目すると、千の位A＋B＝９または、百の位から１繰り上が;；るときA＋B＝８になります。一のくらいから、９＋A＝Bこれは、AはBより１大きいことを意味しています。これより、A＝５、B＝４が決まります。あてはめていくと、C＝０になります。答えA＝５　B＝４　C＝０　D＝９になります。 

夏休み期間中、ホームページに掲載する出来事が少ないです。そこで第1弾として「６０年前の小学校生活」、第２弾として「算数おもしろ問題」を掲載しました。今日は第３弾として、教員歴４０数年間で、ごく一部ですが、心に残っている本の紹介や講演会・研修会等で得た情報を紹介したいと思います。特に「教育に関すること」「子育てに関すること」「人としての方向性を示してくれる言葉に関すること」などを紹介します。ただ、本などは著作権の問題があるので、本の一部を抜粋して紹介することなどは控えさせていただきます。個々で調べてもらったら嬉しいです。

【１回目　子どもが育つ魔法の言葉】

「子どもが育つ魔法の言葉」作：ドロシー・ロー・ノルトを紹介します。ノルトさんは１９２４年アメリカで生まれ、４０年以上にわたって、家庭教育や子育てコンサルタントをされた方です。２００５年に永眠されました。子どもにどんな声かけをすればよいかなど、具体的な言葉でアドバイスをされています。私もいつもこの言葉を胸の中に置いています。検索等をしていただけると幸いです。

今日から８月に入りました。連日の猛暑、今後が心配です。今日は、頭の体操ということで、算数に関したおもしろ問題を出します。家族で楽しんでもらえれば幸いです。今後、数回に分けて出したいと思います。

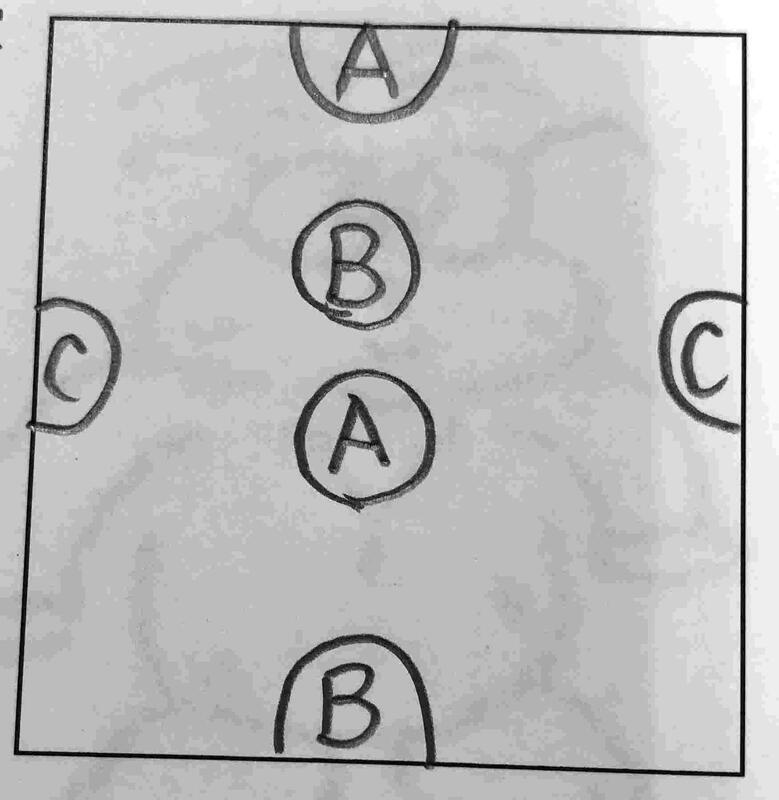
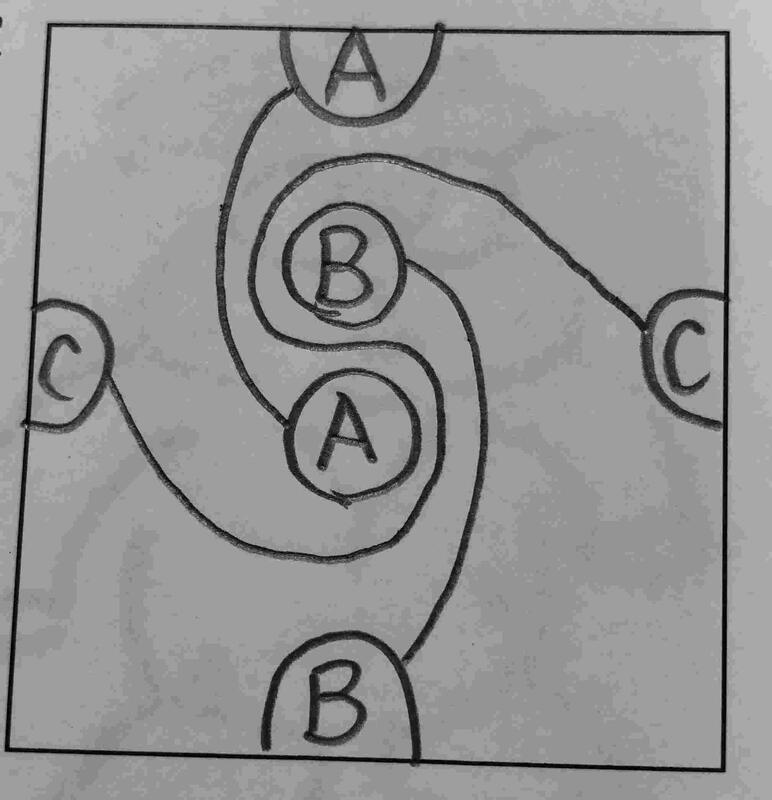
①この問題は、私にとって思い出の問題です。今から約４０数年前、大学を卒業し、最初に５年生４４人を担任しました。その時、子どもたちに出した問題です。慶応幼稚舎（小学校）の入試問題から持ってきています。問題：ⒶとⒶ、ⒷとⒷ、ⒸとⒸを線で結（むす）んでください。ただし、線は交わったり、接したりすることはできません。また、円の中や長方形の外を通ることもできません。

②２年生や３年生のかけ算の時によく使う、とんちかけ算クイズです。

１．はっぱがちってるよ。何枚ちったのかな。

２.　ごごになって、プールに行きました。何人で行ったのかな。

３.　いろんな国をまわってきたよ。いくつの国をまわって来たのかな。

４.　かいすいよくに行って、黒くなって帰って来たよ。何人だったかな。

５.　１００歳になるおばあさんの顔にある、しわは何本かな。

➂単位の学習をする時に使っています。

問題：学校から１０ｍはなれて家が建っています。誰の家でしょうか。

④６年生の線対称の時に使う問題です。

この絵は、ある決まりに従って書いてあります。５番目の絵を想像して描いてみましょう。

 ⑤どんな大きさでもいいので、大小２つのコップを用意してください。問題：ある酒屋では、大きな酒だるからマスで酒の量をはかって売っていました。ただ、マスは９㍑と５㍑がはかれるマスが１つずつしかありません。ある日客がやってきて、「酒を６㍑売ってくれ。」といいました。酒屋の主人は、どのようにして６㍑はかったでしょう。（ただし、酒は酒たるにもどすことができます。）

解答

①

②　１.はっぱ６４まい　２.ごご２５人　３.くに１８か国　４.くろく５４人　５.しわ３２本

➂　１０ｍは㎝になおすと１０００㎝になります。つまりセンセンチ＝せんせんち＝先生家です。

④　数字の１、２、３、４を線対称として描いています。よって「５」を線対称の形にすると下記のようになります。

⑤

５㍑マスに酒を満たし、それを９㍑マスにうつします。次ぎにもう一度５㍑マスに酒を満たし、それを９㍑マスがいっぱいになるまでそそぎます。このとき、９㍑マスにはすでに５㍑の酒が入っているので、４㍑しかそそぐことができません。したがって、５㍑マスには酒が１㍑残ります。いっぱいになった９㍑マスの酒を全部酒だるに戻します。すると、５㍑マスに１㍑の酒が入っている状態になります。からになった９㍑マスへ、５㍑マスに残っていた１㍑の酒をうつしかえます。５㍑マスに酒をみたし、それを９㍑マスにうつしかえます。すると、９㍑マスに酒が６㍑入った状態ができあがります。

いかがだったでしょうか。今後まだまだ続きがありますよ！