よく雨が降りましたね。大丈夫だったでしょうか。今日は８月１２日です。１９８５年（昭和６０年）８月１２日、日航ジャンボ機墜落事故が起きました。亡くなられた方は５２０名でした。今日で丸４０年が経過します。当時、私は教員をしていました。テレビのニュース番組をみて、心がとても痛みました。また、飛行機の制御ができず、左右にぶれることを「ダッチロール」という言葉もこの時、はじめて知りました。４０年の歳月が過ぎましたが、昨日のように思い出します。ご冥福をお祈りいたします。

【算数おもしろ問題】今日の問題も算数オリンピックから引用しています。

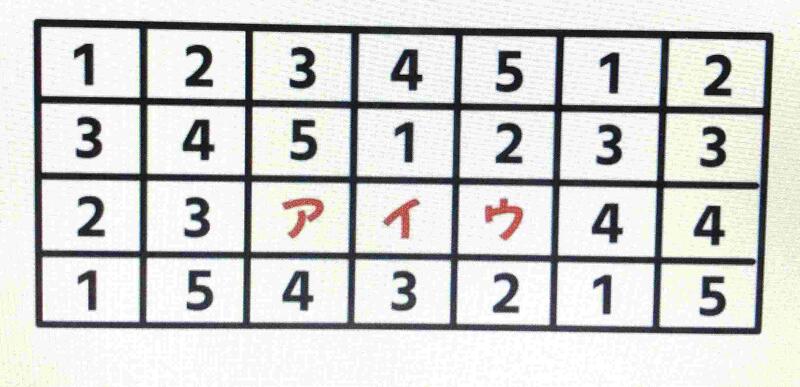
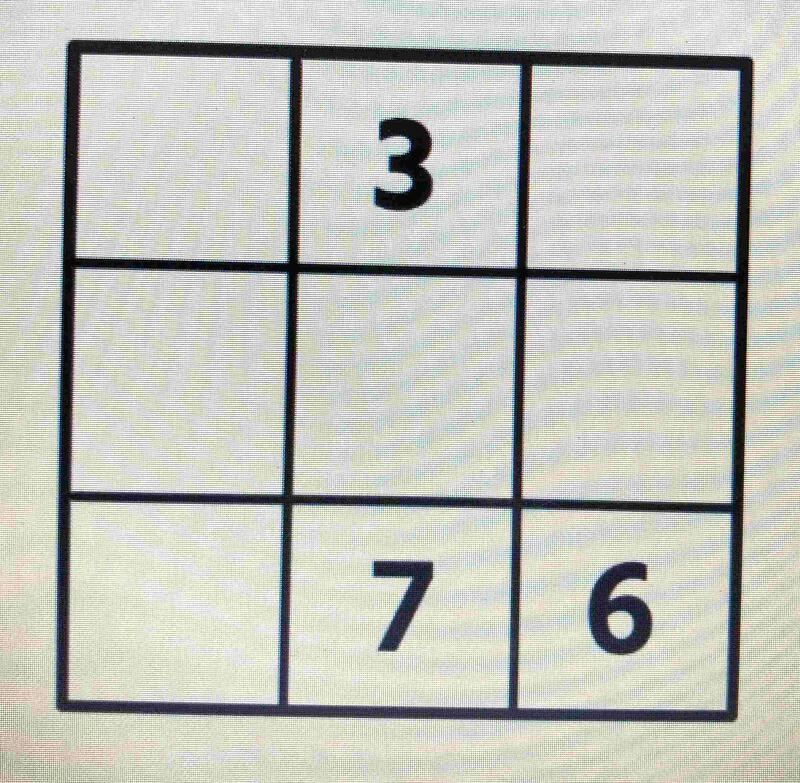
①下の表は、ある法則にしたがって数字が並んでいます。ア、イ、ウに入る数字を考えましょう。

②答えが１０になる２つの式があります。下の記号を使って、それぞれ正しい式にしましょう。（式の計算では、（　　）の中を最初にします。次に✖、÷、最後に＋、－になります。原則計算は左からおこないます。）

 解答

①

②

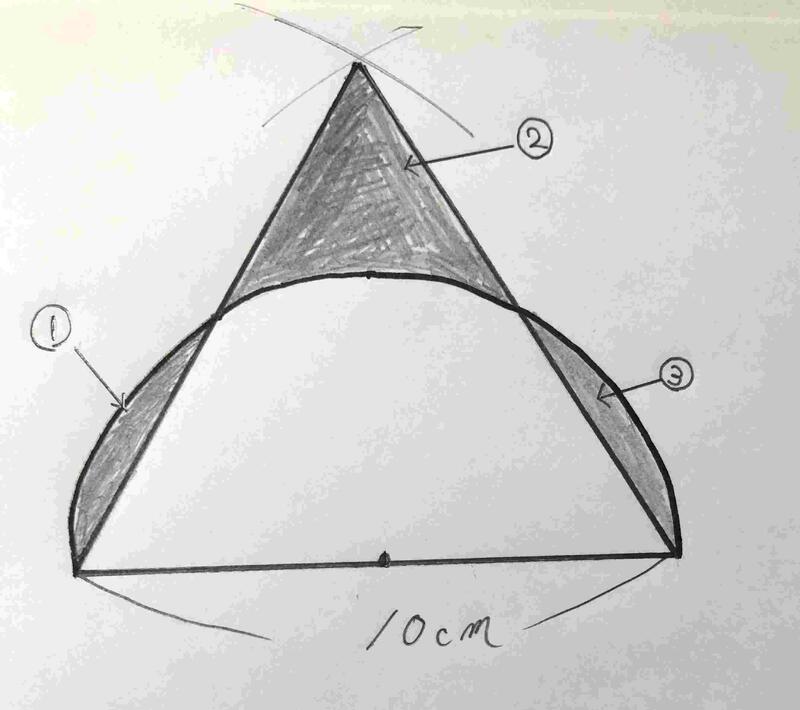
➂等積変形の問題です。下記の図のように１辺の長さが１０ｃｍの正三角形と直径が１０㎝の半円が重なっています。このとき、黒い部分の面積①、②、③を合わせた面積を求めましょう。ただし、円周率は３．１４とします。また、答えは小数第２位を四捨五入して、小数第１位まで求めましょう。

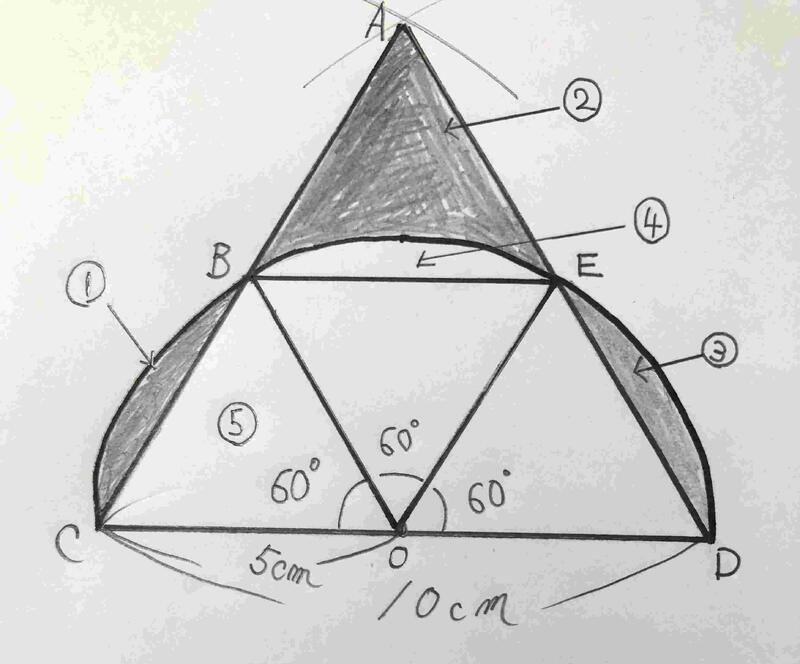
解答➂

まず、半円の中心をOとして、１辺の長さが５㎝の４つの合同（ぴったり重なる）な三角形に分けます。次に③の部分を④に移動させます。三角形ABEの面積になります。三角形ABEの面積と三角形BCOの面積は等しいので、求めたい面積は半径５㎝、中心角６０度の扇形の面積を求めればよいです。よって、５×５×３．１４×６分の１＝１３．０８・・・

答え　約１３．１㎠

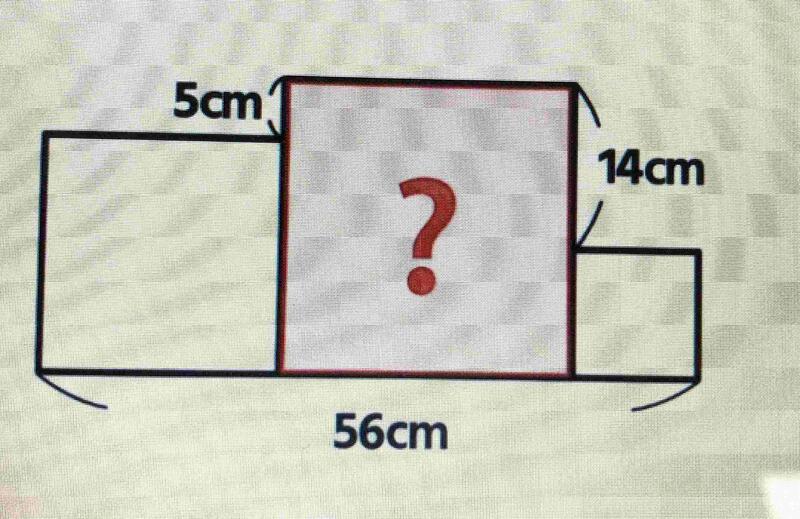
④下記のような３つの正方形があります。真ん中の正方形の１辺は何㎝でしょうか。

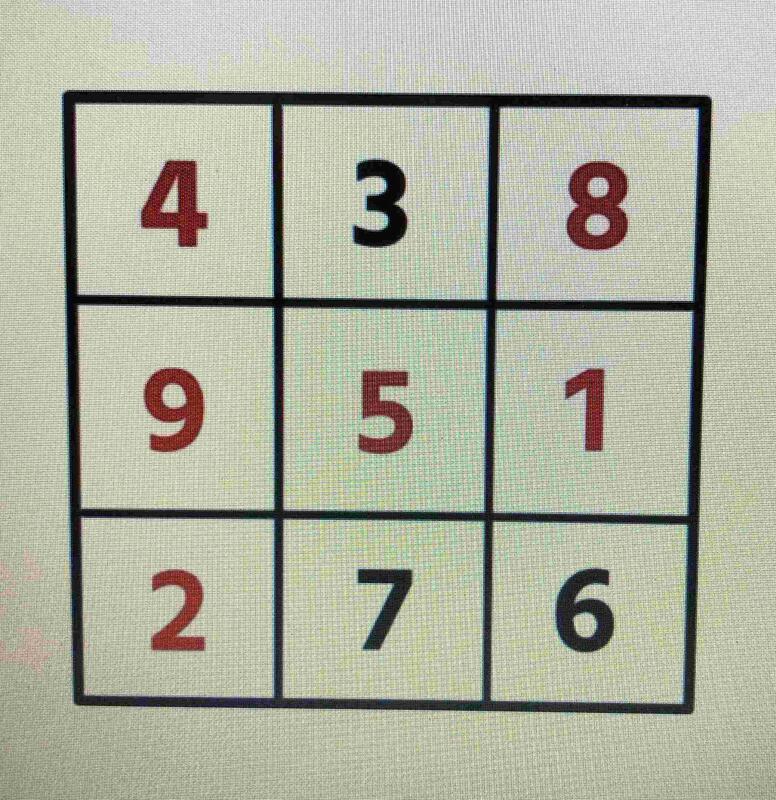
⑤１～９の数字を１つずつ入れて、縦、横、斜め３つの数字の和が同じになるようにしましょう。

解答

④答えの出し方はいろいろあります。その１例です。

中くらいの正方形の１辺の長さをA、１番大きい正方形の１辺の長さをB、１番小さい正方形の１辺の長さをCとおきます。A＋B＋C＝５６、A＝Bー５、Ｃ＝Ｂー１４に置きかえることができます。そこで、Ａ＋Ｂ＋Ｃ＝Ｂ－５＋Ｂ＋Ｂ－１４＝５６。３Ｂー１９＝５６。３Ｂ＝７５。よってＢ＝１５

答え１５㎝

⑤

【７回目　イチロー氏の言葉より】　

一日一日の積み重ねが　みたことのない　世界へつれていってくれる

今日は、日本プロ野球、アメリカ大リーグで活躍された鈴木一郎氏の話をさせていただきます。

最初、私が感銘を受けた言葉は、野球の理論のことです。通常ボールをいかにうまくバットに当てるかを考えます。当時イチロー氏が言った言葉は「２ストライクまで追い込まれたら別だが、それまでは、打ちにいって、自分の考えと違ったボールがきたら、空振りする技術を身につけていると話されました。つまり、打ちにいって、ボテボテのゴロだったらアウトになる確率が高い、それよりも空振りする方が次につながると話されていました。発想の違いを感じました。

先日イチロー氏のアメリカ大リーグ殿堂入りのセレモニーが行われました。すべての人々に対して感謝の気持ちを話されていました。時にはジョークも交えた和やかなスピーチでした。すばらしかったですね。昨年殿堂入りのインタビューを受けられた時、子どもたちに次のようなメッセージを送られていました。

①大きな成果（せいか）をあげるには、いっきにそこへはいけない。地道に毎日をつみ重ねることが、大きな成果をあげる道である。

②人はだれでも才能（さいのう）を持っている。しかし、その才能を花開かせるのは、その人の毎日の努力である。

と話されていました。

５～６年前、現役を引退されたイチロー氏がテレビ出演をされていました。「教えてイチロー先生」というテレビ番組です。イチロー氏が子どもや大人相手に、質問を受け、それに答えていらっしゃいました。その中で、子どもから、こんな質問がありました。「宿題はなぜしなければいけないのですか。」という質問です。それに対しイチロー氏は「私も宿題はいやでした。しかし、大人になってから、いやなことをしなければならないことが沢山あります。その時の練習と思って取り組めばどうでしょうか。」と話されていました。なるほど、一つの考え方ですね。

次にこんな質問もありました。「出る杭は打たれるといいますが、どうすればよいでしょうか。」という質問です。イチロー氏は「出る杭は打たれますが、出すぎる杭は打たれません。」と話されました。この答えを聞いていた時、私は少し顔がほころびました。それは、２０数年前から、私が言ってきたことと、イチロー氏が答えられたことが、一緒だったからです。１０数年間ほぼ毎日、ホームページを更新（こうしん）しています。最初の方は、「そんなことは無駄（むだ）な事」などという声も聞きました。しかし、続けていくとそのような声が小さくなりました。出る杭は打たれます。しかし、出すぎた杭は打たれなくなります。継続は力です。でも、出すぎた時に気をつけなければならないことがあります。それは、謙虚（けんきょ）さが必要になります。出すぎることはいいことですが、同時に謙虚さも兼（か）ね備（そな）えなければいけませんね。

最後に、他人から嫌（きら）われるのは大好きだとも話されていました。一番いやなことは、興味（きょうみ）がないこと、無関心なことが一番つらいと話されました。心にしみる話でした。

【８回目　ひとつのことば　】

北原白秋先生は、１８８５年生誕、１９４２永眠されました。詩人でもあり童謡作家でもあり歌人でもあられました。お母様は熊本の南関町出身の方です。熊本にもゆかりのある方です。「あめあめふれふれ　かあさんが」で知られる「あめふり」など聞かれたことがあるかもしれませんね。白秋先生の作品の中に「ひとつのことば」というものがあります。これは、いかにことばが大切で、いかにことばが人を傷つけるかなど、ことばの大切さが詩の中に凝縮しています。「ひとつのことば」目にしていただくと幸いです。

【９回目　マシュマロ実験】

アメリカのスタンフォード大学で１９７０年代に行われた実験です。４歳の子どもたち１８６人が実験に参加しました。机の上にはさらがあり、マシュマロが１このっています。実験者は「私はちょっと用がある。それはきみにあげるけど、私がもどってくるまで１５分間、食べるのをがまんしていたら、マシュマロをもう１つあげる。私がいない間に食べたら、２つめはなしだよ」と言って部屋を出て行きました。最後までがまんして、２こめのマシュマロを手に入れた子どもは３分の１程度でした。

その後ついせき調査をし、マシュマロを食べなかったグループは、まわりから、より優秀と評価され、大学進学適性試験でも点数がよかったそうです。この傾向が、ずっと後の人生に継続していることがあきらかにされました。（生涯年収もよかったそうです。）

自分の衝動（しょうどう）や感情をコントロールし、目先の欲求（よっきゅう）をしんぼうする能力（のうりょく）は、人が社会で成功するうえで、重要であることを意味している実験です。がまんできることは、その人が将来よりよい人生をおくるのに重要なことを言っています。

すべて「がまん・がまん」ではありませんが、がまんする気持ちはその人を大きく成長させる行動ですね。